Il y a des méthodes mathématiques qui, à première vue, semblent presque magiques. La méthode de Monte-Carlo fait partie de celles-ci. Derrière son nom évocateur de casino se cache une technique puissante, utilisée aussi bien en mathématiques qu’en physique, en finance ou en intelligence artificielle. Et pourtant, son principe est d’une simplicité déconcertante : utiliser le hasard pour approcher des résultats impossibles à calculer précisément autrement.
Un jeu de hasard… pour approcher π
Imaginez un carré de côté 1. À l’intérieur de ce carré, on trace un quart de cercle de rayon 1, dont l’aire vaut :
\(\text{Aire du quart de cercle} = \frac{\pi}{4}\)
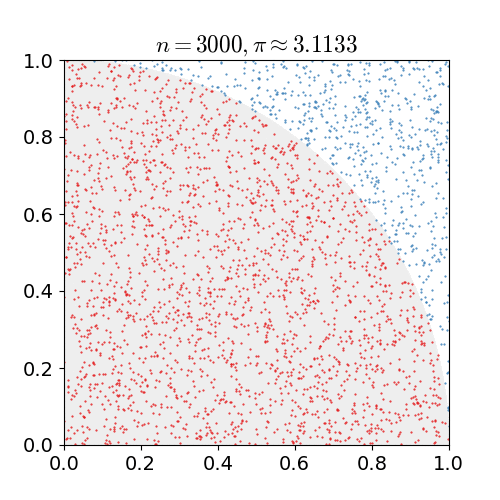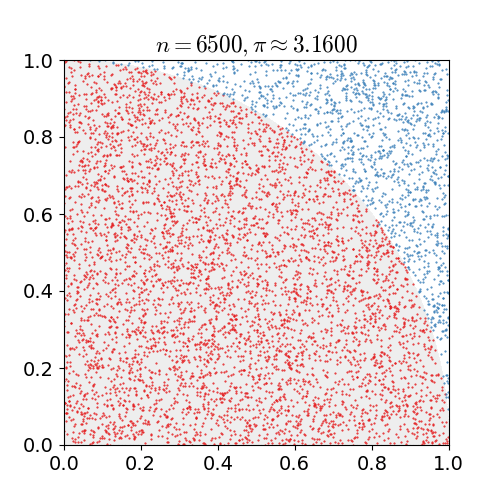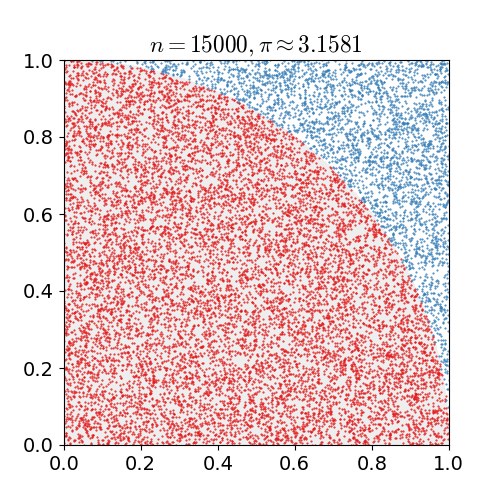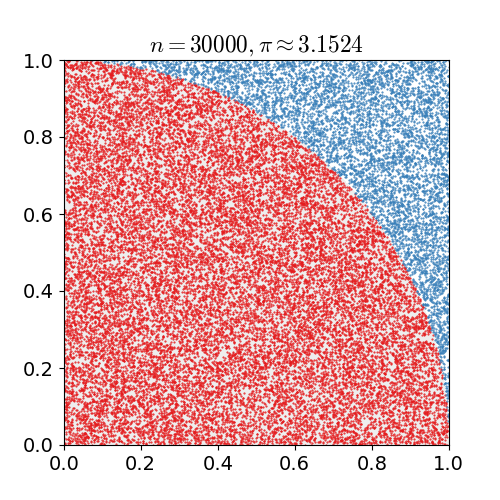
Le principe : on “lance” des points au hasard dans le carré. Certains tombent à l’intérieur du quart de cercle, d’autres à l’extérieur.
En comptant le nombre de points qui “réussissent” (c’est-à-dire qui tombent dans le quart de cercle), on peut approcher la valeur de π.
Pourquoi ça marche ?
La proportion de points à l’intérieur du quart de cercle, rapportée au nombre total de points dans le carré, donne une estimation de l’aire du quart de cercle, donc de π.
\[\frac{\text{Points dans le quart de cercle}}{\text{Points dans le carré}} \approx \frac{\text{Aire du quart de cercle}}{\text{Aire du carré}} = \frac{\pi}{4}\]Il suffit alors de multiplier ce rapport par 4 pour obtenir une approximation de π :
\[\pi \approx 4 \times \frac{\text{Points dans le quart de cercle}}{\text{Nombre total de points}}\]Implémentation en OCaml
Rien de tel que de passer à la pratique ! Voici un programme OCaml qui applique cette méthode :
let monte_carlo iterations =
let rec monte_carlo2 reste total =
match reste with
| 0 -> let pi = 4. *. float_of_int total /. float_of_int iterations in
pi
| _-> let x = Random.float 1. in
let y = Random.float 1. in
let in_circle = if x *. x +. y *. y <= 1. then
1
else
0
in
monte_carlo2 (reste-1) (total+in_circle)
in
monte_carlo2 iterations 0
Signature du programme :
val monte_carlo : int -> float = <fun>
Expérimentons : la magie (et la limite) du hasard
Essayons la fonction avec différents nombres de points :
# monte_carlo 500
- : float = 3.136
# monte_carlo 5000
- : float = 3.1856
# monte_carlo 50000
- : float = 3.14544
# monte_carlo 500000
- : float = 3.140144
On observe que plus on augmente le nombre de “lancers”, plus l’approximation de π se rapproche de la valeur réelle (3.14159…).
Mais il y a une limite : même avec 10 millions de points, on n’obtient que 3 à 4 décimales correctes. C’est la rançon du hasard : la précision augmente lentement avec le nombre de points.
Pourquoi utiliser Monte-Carlo ?
La méthode de Monte-Carlo est utilisée partout où il est difficile, voire impossible, de calculer une valeur de façon exacte.
Elle est précieuse pour :
- Estimer des intégrales complexes
- Simuler des phénomènes physiques (diffusion, réactions nucléaires…)
- Modéliser des marchés financiers
- Tester des algorithmes d’intelligence artificielle
Son principal atout : la simplicité d’implémentation, même pour des problèmes très complexes.
Essayez par vous-même !
Vous pouvez tester ce code directement dans votre compilateur ou interpréteur OCaml (ocamlc, ocamlopt) ou en ligne sur :
https://try.ocamlpro.com/
Conseil : Essayez de modifier le nombre d’itérations, ou d’imaginer d’autres figures géométriques à “viser” avec des points aléatoires. La méthode de Monte-Carlo n’a de limite que votre imagination !
La beauté de Monte-Carlo, c’est que même le hasard, bien utilisé, peut révéler l’ordre caché du monde…